Функциональная отделимость

Вы находитесь на сайте "Архив статей из ЭЕЭ и статей на еврейские темы из Википедии"

Версия 21:25, 22 ноября 2010 (просмотреть исходный код) MyBot (Обсуждение | вклад) (Delete this category, not in RUB) ← Предыдущая правка		Версия 14:40, 30 ноября 2010 (просмотреть исходный код) MyBot (Обсуждение | вклад) (Delete this category, not in RUB) Следующая правка →
Строка 28:		Строка 28:
	{{WikiCopyRight}}		{{WikiCopyRight}}
-	{{checked}}	+
		+	[[Категория:требует категоризации]]{{checked_final}}

---

Версия 14:40, 30 ноября 2010

Тип статьи:	Регулярная статья

Два подмножества A и B в данном топологическом пространстве X называются функционально отделимыми в X, если существует такая определенная во всём пространстве вещественная ограниченная непрерывная функция f, которая принимает во всех точках множества A одно значение a, a во всех точках множества B ― некоторое отличное от a значение b. При этом всегда можно предположить, что 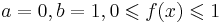во всех точках .

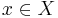Пространство, в котором всякая точка функционально отделима от всякого не содержащего её замкнутого множества, называется вполне регулярным.

Свойства

• Два функционально отделимых множества всегда отделимы и окрестностями. Обратное утверждение верно не всегда, однако имеет место:
  • Лемма Урысона. В нормальном пространстве всякие два дизъюнктные замкнутые множества функционально отделимы.

См. также

• Принцип разделимости

Уведомление: Предварительной основой данной статьи была аналогичная статья в http://ru.wikipedia.org, на условиях CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0, которая в дальнейшем изменялась, исправлялась и редактировалась.