Хаусдорфово пространство
Вы находитесь на сайте "Архив статей из ЭЕЭ и статей на еврейские темы из Википедии"
Architect (Обсуждение | вклад) м (Замена текста — «}} '''» на «}}'''») |
MyBot (Обсуждение | вклад) (Delete this category, not in RUB) |
||
| Строка 40: | Строка 40: | ||
{{нет источников}} | {{нет источников}} | ||
| - | + | ||
[[ar:فضاء هاوسدورف]] | [[ar:فضاء هاوسدورف]] | ||
Версия 20:40, 24 октября 2010
| Регулярная статья | |
Хаусдорфовыми пространствами называются топологические пространства, удовлетворяющие сильной аксиоме отделимости. Названы в честь Ф. Хаусдорфа, одного из основоположников общей топологии. Его первоначальное определение топологического пространства включало в себя требование, которое теперь называется хаусдорфовостью. Иногда для обозначения структуры хаусдорфового топологического пространства на множестве применяется термин хаусдорфова топология.
Определение
Топологическое пространство X называется хаусдорфовым, если любые две различных точки x, y из X обладают непересекающимися окрестностями U(x), V(y).
Примеры и контрпримеры
- Хаусдорфовы
- Хаусдорфовыми являются все метрические пространства и метризуемые пространства, в частности:
- евклидовы пространства
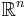
- многообразия
- большинство используемых в анализе бесконечномерных функциональных пространств, таких как
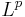или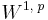 
, 
.
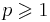- евклидовы пространства
- По определению, топологические группы являются хаусдорфовыми.
- Хаусдорфовыми являются все метрические пространства и метризуемые пространства, в частности:
- Нехаусдорфовы
- Не является хаусдорфовой, например, топология Зарисского на алгебраическом многообразии.
- Нехаусдорфов, вообще говоря, спектр кольца.
- Простейший (и важный) пример нехаусдорфова пространства — связное двоеточие, а в более общем случае — алгебры Гейтинга.
Свойства
- Единственность предела последовательности (в более общем случае — фильтра), если таковой предел существует.
- Свойство, равносильное определению хаусдорфовости топологии, — замкнутость диагонали
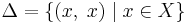в декартовом квадрате 
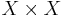пространства X. - В хаусдорфовом пространстве замкнуты все его точки (то есть одноточечные множества).
- Подпространство и декартово произведение хаусдорфовых пространств тоже хаусдорфовы.
- Вообще говоря, хаусдорфовость не передаётся факторпространствам.
 |
В этой статье не хватает ссылок на источники информации.
Информация должна быть по возможности подкреплена ссылками, это увеличивает авторитетность материалов Ежевики.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. |
ar:فضاء هاوسدورف ca:Espai de Hausdorff cs:Hausdorffův prostor cv:Хаусдорф уçлăхĕ da:Hausdorffrumet:Hausdorffi ruum fa:فضای هاسدورف fi:Hausdorffin avaruusja:ハウスドルフ空間 ko:하우스도르프 공간 mn:Хаусдорфын огторгуй nl:Hausdorff-ruimte pl:Przestrzeń Hausdorffa pt:Espaço de Hausdorff sk:Hausdorffov priestor sv:Hausdorffrum tr:Hausdorff uzayzh:豪斯多夫空间
Уведомление: Предварительной основой данной статьи была аналогичная статья в http://ru.wikipedia.org, на условиях CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0, которая в дальнейшем изменялась, исправлялась и редактировалась.
