Теорема Крейна — Мильмана

Вы находитесь на сайте "Архив статей из ЭЕЭ и статей на еврейские темы из Википедии"

Версия 13:59, 3 января 2012 (просмотреть исходный код) Л.Гроервейдл (Обсуждение | вклад) м (убрана категория «Требует категоризации»; добавлена категория «Евреи в СССР» с помощью HotCat) ← Предыдущая правка		Версия 14:00, 3 января 2012 (просмотреть исходный код) Л.Гроервейдл (Обсуждение | вклад) (→Литература) Следующая правка →
Строка 32:		Строка 32:
	{{math-stub}}		{{math-stub}}
-		+	{{WikiCopyRight}}
-		+
-		+
-		+
-	[[de:Satz von Krein-Milman]]	+
-	[[en:Krein–Milman theorem]]	+
-	[[fr:Théorème de Krein-Milman]]	+
-	[[it:Teorema di Krein-Milman]]	+
-	[[ko:크레인-밀만 정리]]	+
-	[[pl:Twierdzenie Kreina-Milmana]]{{WikiCopyRight}}	+
	/math		/math
	[[Категория:Евреи в СССР]]		[[Категория:Евреи в СССР]]

---

Версия 14:00, 3 января 2012

Тип статьи:	Текст унаследован из Википедии

Теорема Крейна — Мильмана — важный факт из выпуклого анализа в линейных топологических пространствах. Для бесконечномерных пространств данная теорема, как и многие другие результаты, не может быть доказана без применения аксиомы выбора или эквивалентных ей утверждений теории множеств.

Шаблон:Рамка пусть L — локально-выпуклое пространство, K — выпуклый компакт в L, E — совокупность крайних точек K. Тогда K совпадает с замыканием выпуклой оболочки множества E. Шаблон:/рамка Доказана советскими математиками Марком Григорьевичем Крейном и Давидом Пинхусовичем Мильманом (1940).

Доказательство

Пусть H — выпуклая оболочка крайних точек K. Так как K компактно и выпукло, то замыкание Поэтому 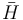компактно. Предположим, что некоторая точка 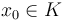и 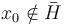. Применяя теорему Хана — Банаха к x₀ и 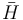, показать, что 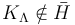( — теорема Хана — Банаха). Таким образом мы получаем противоречие построению .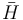

Теорема доказана.

Одно из приложений этой теоремы — доказательство неизоморфности различных банаховых пространств; другое — изящное доказательство де Бранжа теоремы Стоуна — Вейерштрасса.

Литература

• Кириллов А.А., Гвишиани А.Д. Теоремы и задачи функционального анализа, 1988.

Шаблон:Math-stub

Уведомление: Предварительной основой данной статьи была аналогичная статья в http://ru.wikipedia.org, на условиях CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0, которая в дальнейшем изменялась, исправлялась и редактировалась. /math