Теорема Шура
Вы находитесь на сайте "Архив статей из ЭЕЭ и статей на еврейские темы из Википедии"
(Различия между версиями)
Karkaix (Обсуждение | вклад) (Новая страница: «'''Теорема Шура''' {{рамка}} Пусть <math>M</math> — связное (возможно не [[пол…») |
MyBot (Обсуждение | вклад) (Add template остатье) |
||
| Строка 1: | Строка 1: | ||
| - | '''Теорема Шура''' | + | {{Остатье| ТИП СТАТЬИ = 1 |
| + | | АВТОР1 = | ||
| + | | АВТОР2 = | ||
| + | | АВТОР3 = | ||
| + | | СУПЕРВАЙЗЕР = | ||
| + | | ПРОЕКТ = | ||
| + | | ПОДТЕМА = | ||
| + | | КАЧЕСТВО = | ||
| + | | УРОВЕНЬ = | ||
| + | | ДАТА СОЗДАНИЯ = | ||
| + | | ВИКИПЕДИЯ = | ||
| + | | НЕОДНОЗНАЧНОСТЬ = | ||
| + | }}'''Теорема Шура''' | ||
{{рамка}} | {{рамка}} | ||
Пусть <math>M</math> — [[связное пространство|связное]] (возможно не [[полное пространство|полное]]) [[риманово многообразие]] | Пусть <math>M</math> — [[связное пространство|связное]] (возможно не [[полное пространство|полное]]) [[риманово многообразие]] | ||
Версия 10:02, 18 апреля 2010
| Регулярная статья | |
Теорема Шура Шаблон:Рамка Пусть M — связное (возможно не полное) риманово многообразие размерности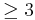 
. Если секционная кривизна 
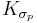, где σp есть плоскость в Tp(M), зависит только от p, то M есть пространство постоянной кривизны. Шаблон:/рамка
Литература
- с. 192, Ш. Кобаяси, К. Номидзу, Основы Дифференциальной геометрии
- Schur F. Über den Zusammenhang der Räume konstanter Krümmungsmasses mit den projektiven Räuraen, Mathematische Annalen, 1886. 27, S. 537—567.sv:Schurs sats
Уведомление: Предварительной основой данной статьи была аналогичная статья в http://ru.wikipedia.org, на условиях CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0, которая в дальнейшем изменялась, исправлялась и редактировалась.
