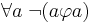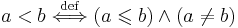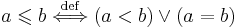Частично упорядоченное множество

Вы находитесь на сайте "Архив статей из ЭЕЭ и статей на еврейские темы из Википедии"

(Различия между версиями)
Перейти к: навигация, поиск
(Delete this category, not in RUB)
м (убрана категория «Требует категоризации» с помощью HotCat)
Строка 224: Строка 224:
{{WikiCopyRight}}
{{WikiCopyRight}}
-
[[Категория:требует категоризации]]{{checked_final}}
+
{{checked_final}}

Версия 16:32, 1 сентября 2011

Тип статьи: Регулярная статья
Файл:Hasse diagram of powerset of 3.svg
Подмножества {x, y, z}, упорядоченные отношением включения

Частично упорядоченное множество — математическое понятие, которое формализует интуитивные идеи упорядочивания, расположения в определенной последовательности и т. п. Неформально говоря, множество частично упорядочено, если указано, какие элементы следуют (больше и т. п.) за какими. При этом в общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».

В качестве абстрактного примера можно привести совокупность подмножеств множества из трех элементов {x,y,z}, упорядоченное по отношению включения.

В качестве примера «из жизни» можно привести множество людей, упорядоченное по отношению «быть предком».

Содержание

Определение и примеры

Порядком, или частичным порядком, на множестве M называется бинарное отношение 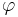\varphi на M (определяемое некоторым множеством 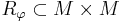R_{\varphi} \subset M \times M ), удовлетворяющее следующим условиям[1]:

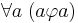
  • Рефлексивность: \forall a \; (a \varphi a)
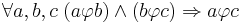
  • Транзитивность: \forall a, b, c \; (a \varphi b) \wedge (b \varphi c) \Rightarrow a \varphi c
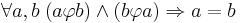
  • Антисимметричность: \forall a, b \; (a \varphi b) \wedge (b \varphi a) \Rightarrow a = b

Множество M, на котором задано отношение частичного порядка, называется частично упорядоченным (англ. partially ordered set, poset). Если быть совсем точным[2], то частично упорядоченным множеством называется пара 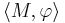\langle M, \varphi \rangle, где M — множество, а 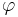\varphi — отношение частичного порядка на M.

Терминология и обозначения

Отношение частичного порядка обычно обозначают символом 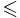\leqslant, по аналогии с отношением «меньше либо равно» на множестве действительных чисел. При этом, если 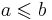a \leqslant b, то говорят, что элемент a не превосходит b, или что a подчинен b.

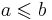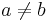Если a \leqslant b и a \neq b, то пишут a < b, и говорят, что a меньше b, или что a строго подчинен b.

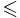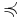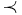Иногда, чтобы отличить произвольный порядок на некотором множестве от известного отношения «меньше либо равно» на множестве действительных чисел, вместо \leqslant и < используют специальные символы \preccurlyeq и \prec соответственно.

Строгий и нестрогий порядок

Отношение, удовлетворяющее условиям рефлексивности, транзитивности и антисимметричности, также называют нестрогим, или рефлексивным порядком. Если условие рефлексивности заменить на условие антирефлексивности:

\forall a \; \neg (a \varphi a)

то получим определение строгого, или антирефлексивного порядка.

Если 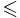\leqslant — нестрогий порядок на множестве M, то отношение < , определяемое как:

a < b \; \overset{\mathrm{def}}{\Longleftrightarrow} \; (a \leqslant b) \wedge (a \neq b)

является строгим порядком на M. Обратно, если < — строгий порядок, то отношение 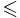\leqslant, определенное как

a \leqslant b \; \overset{\mathrm{def}}{\Longleftrightarrow} \; (a < b) \vee (a = b)

является нестрогим порядком.

Поэтому все равно — задать на множестве нестрогий порядок, или строгий порядок. В результате получится одна и та же структура. Разница только в терминологии и обозначениях.

Примеры

Файл:Hasse diagram of powerset of 3.svg
Подмножества {x, y, z}, упорядоченные отношением включения

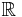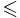\vartriangleright Как уже указывалось выше, множество действительных чисел \mathbb{R} частично упорядочено по отношению «меньше либо равно» \leqslant.

\vartriangleright Пусть M — множество всех действительнозначных функций, определенных на отрезке [a,b], то есть функций вида

f \colon [a,b] \to \mathbb{R}

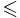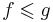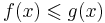Введем отношение порядка \leqslant на M следующим образом. Мы скажем, что f \leqslant g, если для всех x \in [a,b] выполнено неравенство f(x) \leqslant g(x). Очевидно, введенное отношение в самом деле является отношение частичного порядка.

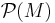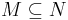\vartriangleright Пусть M — некоторое множество. Множество \mathcal{P}(M) всех подмножеств M (так называемый булеан), частично упорядочено по включению M \subseteq N.

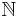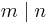\vartriangleright Множество всех натуральных чисел \mathbb{N} частично упорядочено по отношению делимости m \mid n.

Связанные определения

Несравнимые элементы

Если a и b — действительные числа, то имет место одно и только из соотношений:

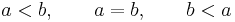
a < b, \qquad a=b, \qquad b<a

В случае, если a и b — элементы произвольного частично упорядоченного множества, то существует четвёртая логическая возможность: не выполнено ни одно из указанных трех соотношений. В этом случае элементы a и b называются несравнимыми. Например, если M — множество действительнозначных функций на отрезке [0,1], то элементы f(x) = x и g(x) = 1 − x будут несравнимы. Возможность существования несравнимых элементов объясняет смысл термина «частично упорядоченное множество».

Минимальный/максимальный и наименьший/наибольший элементы

Основные статьи: Максимум (математика), Минимум (математика)

Из-за того, что в частично упорядоченном множестве могут быть пары несравнимых элементов, вводятся два различных определения: минимального элемента и наименьшего элемента.

Элемент 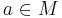a \in M называется минимальным (англ. minimal element), если не существует элемента b < a. Другими словами, a — минимальный элемент, если для любого элемента 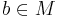b \in M либо b > a, либо b = a, либо b и a несравнимы. Элемент a называется наименьшим (англ. least element, lower bound (opp. upper bound)), если для любого элемента 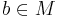b \in M имеет место неравенство 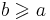b \geqslant a. Очевидно, всякий наименьший элемент является также минимальным, но обратное в общем случае неверно: минимальный элемент a может и не быть наименьшим, если существуют элементы b, не сравнимые с a.

Очевидно, что если в множестве существует наименьший элемент, то он единственен. А вот минимальных элементов может быть несколько. В качестве примера рассмотрим множество 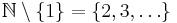\mathbb{N}\setminus \{ 1 \} = \{ 2, 3, \ldots \} натуральных чисел без единицы, упорядоченное по отношению делимости 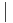\mid. Здесь минимальными элементами будут простые числа, а вот наименьшего элемента не существует.

Аналогично вводятся понятия максимального (англ. maximal element) и наибольшего (англ. greatest element) элементов.

Верхние и нижние грани

Пусть A — подмножество частично упорядоченного множества 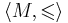\langle M, \leqslant\rangle. Элемент 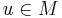u \in M называется верхней гранью (англ. upper bound) A, если любой элемент 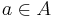a \in A не превосходит u. Аналогично вводится понятие нижней грани (англ. lower bound) множества A.

Любой элемент, больший, чем некоторая верхняя грань A, также будет верхней гранью A. А любой элемент, меньший, чем некоторая нижняя грань A, также будет нижней гранью A. Эти соображения ведут к введению понятий наименьшей верхней грани (англ. least upper bound) и наибольшей нижней грани (англ. greatest lower bound).

Специальные типы частично упорядоченных множеств

Линейно упорядоченные множества

Основная статья: Линейно упорядоченное множество

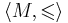Пусть \langle M, \leqslant\rangle — частично упорядоченное множество. Если в M любые два элемента сравнимы, то множество M называется линейно упорядоченным (англ. linearly ordered set). Линейно упорядоченное множество также называют совершенно упорядоченным (англ. totally ordered set), или просто, упорядоченным множеством[3]. Таким образом, в линейно упорядоченном множество для любых двух элементов a и b имеет место одно и только одно из соотношений: либо a < b, либо a = b, либо b < a.

Также всякое линейно упорядоченное подмножество частично упорядоченного множества называют цепью (англ. chain), то есть цепь в частично упорядоченном множестве 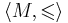\langle M, \leqslant \rangle — такое его подмножество, в котором любые два элемента сравнимы.

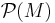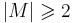Из приведенных выше примеров частично упорядоченных множеств только множество действительных чисел является линейно упорядоченным. Множество действительнозначных функций на отрезке [a,b] (при условии a < b), булеан \mathcal{P}(M) (при |M|\geqslant 2), натуральные числа с отношением делимости — не являются линейно упорядоченными.

В линейно упорядоченном множестве понятия наименьшего и минимального, а также наибольшего и максимального, совпадают.

Вполне упорядоченные множества

Основная статья: Вполне упорядоченное множество

Линейно упорядоченное множество называется вполне упорядоченным (англ. well-ordered), если каждое его непустое подмножество имеет наименьший элемент[4]. Соответственно, порядок на множестве называется полным порядком (англ. well-order).

Классический пример вполне упорядоченного множества — множество натуральных чисел 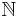\mathbb{N}. Утверждение о том, что любое непустое подмножество 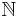\mathbb{N} содержит наименьший элемент, равносильно принципу математической индукции. В качестве примера линейно упорядоченного, но не вполне упорядоченного множества можно привести множество неотрицательных чисел 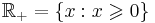\mathbb{R}_{+} = \{ x: x \geqslant 0\}. Действительно, его подмножество {x:x > 1} не имеет наименьшего элемента.

Вполне упорядоченные множества играют исключительно важную роль в общей теории множеств.

Теоремы о частично упорядоченных множествах

К числу фундаментальных теорем о частично упорядоченных множествах относятся принцип максимума Хаусдорфа и лемма Куратовского-Цорна. Эти утверждения эквивалентны между собой и существенно опираются на так называемую аксиому выбора (в действительности, эквивалентны аксиоме выбора).

Примечания

  1. ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2004. — С. 36. — 572 с. — ISBN 5-9221-0266-4
  2. ↑ Александров П. С. Введение в теорию множеств и общую топологию. — М.: «НАУКА», 1977. — С. 78. — 368 с.
  3. ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2004. — С. 38. — 572 с. — ISBN 5-9221-0266-4
  4. ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2004. — С. 40. — 572 с. — ISBN 5-9221-0266-4

Литература

  • Александров П. С. Введение в теорию множеств и общую топологию. — М.: «НАУКА», 1977. — 368 с.
  • Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2004. — 572 с. — ISBN 5-9221-0266-4
  • Хаусдорф Ф. Теория множеств. — 4-е изд. — М.: УРСС, 2007. — 304 с. — ISBN 978-5-382-00127-2

См. также

  • Решетка
  • Порядковое число
  • Предпорядок


cs:Uspořádaná množinaeo:Partordohu:Részbenrendezett halmazko:부분순서 nl:Partiële orde oc:Relacion d'òrdre ro:Relaţie de ordine sl:Relacija urejenostizh:偏序关系

Уведомление: Предварительной основой данной статьи была аналогичная статья в http://ru.wikipedia.org, на условиях CC-BY-SA, http://creativecommons.org/licenses/by-sa/3.0, которая в дальнейшем изменялась, исправлялась и редактировалась.


Источник — «http://www.jearc.info/wiki/%D0%A7%D0%B0%D1%81%D1%82%D0%B8%D1%87%D0%BD%D0%BE_%D1%83%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BE%D1%87%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE»
Личные инструменты
 

Шаблон:Ежевика:Рубрики

Навигация